Ptychography

(Top)

Ptychography is an computational imaging technique built on methods from scanning transmission electron/X-ray microscopy (STE/XM) and coherent diffraction imaging (CDI) (1,2). A ptychography experiment records multiple interference patterns from overlapping illuminations of a sample, and solves the phase problem to reconstruct a complex image of the sample. Ptychography has proven experimentally successful with both X-rays (3–5) and electrons (6–8), achieving record-breaking resolutions.

Implementations of ptychography may vary considerably in the choice of inverse solver algorithms and the methods they use to achieve stronger experimental robustness. However, they all share the common notion of overlapping illuminations by known probe positions.

Experimental setup

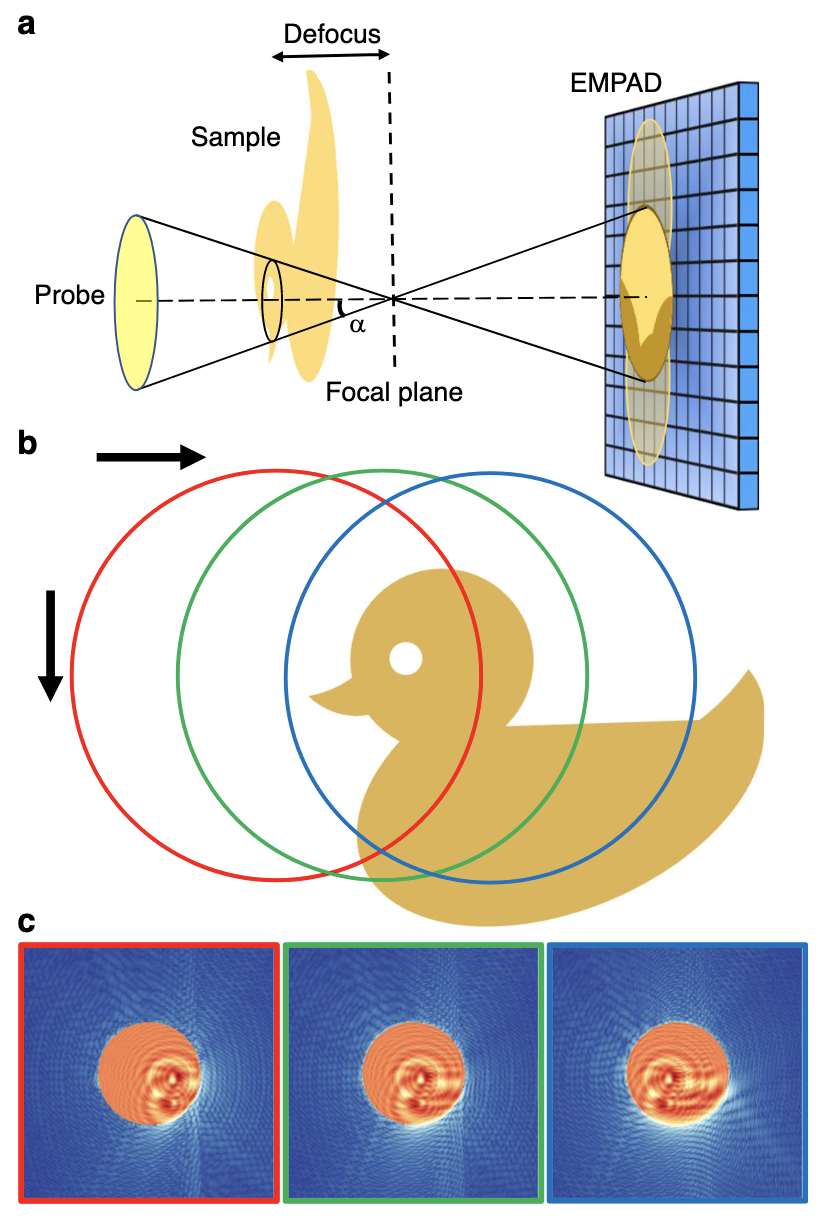
Schematic of defocused probe electron ptychography.
a Experimental setup. The focus of the electron probe is downstream from the sample at a distance defined by the defocus value. The diffraction pattern on the detector (EMPAD) shows a shadow image in the bright-field disk. b A diagram of the scan procedure. c Three diffraction patterns simulated when the probe is illuminated at the positions circled in b, which show the shadow images in the bright-field disk shifting accordingly with the probe position. The speckles in the dark-field region contain high frequency information.

figure from (9).

A basic ptychographic experiment consists of a a focused beam (probe) scanned across a sample of interest. As in the schematic above, the probe illuminates a portion of the sample, which is propagated to a pixel array detector where a macroscopic interference pattern is recorded. In this sense, ptychography closely resembles (and is often called a form of) CDI.

However, an important distinction is that ptychography does not require the usual oversampling condition fundamental to CDI (1). Instead, ptychography requires that the probe shifts laterally to illuminate another overlapping portion of the sample. These overlapping “views” and their corresponding interference patterns make a 4D dataset, a method familiar to 4D-STEM (10).

The final (and arguably the most important) step is to recover the phase part of the interference patterns and reconstruct the sample. This is done computationally, with many algorithms being adopted from conventional phase retrieval in CDI to accomodate for the probe shifts. Recent successes in ptychography have used iterative algorithms, while also developing methods for robustness against experimental error and faster convergence (1).

Basic mathematical model

Notation

• Coordinates
  • Real-space coordinates: \(\mathbf{x}\)
  • Reciprocal-space coordinates: \(\mathbf{k}\)
• Reconstruction
  • The “object” (sample): \(O\)
  • The “probe”: \(P\)
  • The reconstructions are denoted with a carat: \(\hat{O}\), \(\hat{P}\)
  • The \(n\)th iteration is in parentheses: \(\hat{O}^{(n)}\), \(\hat{P}^{(n)}\)
  • The scan positions are indexed with \(j\): \(\mathbf{X}_j\)
  • The exit waves: \(\psi_j(\mathbf{x})\)
  • The measured intensities: \(I_j(\mathbf{k})\)

To build a reconstruction algorithm, we must have a mathematical model of the experiment. The core of ptychography can be summarised as:

1. The decomposition of the exit wave \(\psi\) as a product of the object \(O\) and a focused probe \(P\).
2. The lateral shifts \(\mathrm{X}_j\) between the object \(O\) and probe \(P\).

Expressed as an equation, these conditions say:

\[ \psi_j(\mathbf{x}) = O(\mathbf{x}) \cdot P(\mathbf{x} - \mathbf{X}_j) \]

The exit waves propagate to the detector plane, where the interference patterns are recorded but the phase is lost. Assuming Fraunhofer diffraction, this is the modulus squared of its Fourier transform.

\[ I_j(\mathbf{k}) = |\tilde{\psi}_j(\mathbf{k})|^2 = | \mathcal{F} [\psi_j(\mathbf{x})] |^2 \]

These two equations roughly represent the constraints that let us solve the phase problem; each in the real domain and reciprocal domain respectively.

Reconstruction algorithms

Modelling the forward propagation is simple; however, going backwards is tricky. This is an inverse problem, where one wants to recover the object function \(\hat O\) constrained by the known interference measurements \(I_j\) and scan positions \(\mathbf{X}_j\). Perhaps surprisingly, the real space constraint of shifting illuminations provides enough information for the solution to be well-behaved (1). Here I will restate a brief history and survey of ptychography algorithms given by Rodenburg and Maiden in (1). Detailed explanation with code examples can (hopefully, in the future) be found by following the links.

Inverse solvers

The first type (called Class 1 by Rodenburg and Maiden) of algorithms are those that directly solve for the phases. Originally, ptychography was coined in 1970 by Hergel and Hoppe (11), where they introduced a method of phase retrieval by exploiting the excess information in overlapping Bragg disks of a crystal diffraction experiment. However, this has little to do with modern ptychography, which uses overlap in real space instead. This line of reasoning started with Bates and Rodenburg (12,13) by attempting an analytic solution, called Wigner Distribution Deconvolution (WDD).

Beginning with the Ptychographic Iterative Engine (PIE) algorithm by Rodenburg and Faulkner (14), iterative methods for ptychography started gaining popularity. PIE is a natural extension of conventional CDI phase retrieval algorithms that solve for a ptychographic dataset, where the additional constraint of overlap was suggested to improve convergence.

After PIE, Guizar-Sicairos and Fienup developed a Conjugate Gradient Descent (CGD) method (15), that solves globally rather than piecewise like PIE. Another independent method was introduced by Thibault et al. based on set projection, the Difference Map (DM) (16). CGD and DM allowed the simultaneous reconstruction of the object and probe, an important feature of modern ptychography algorithms and one that improves experimental robustness significantly. PIE was improved to solve for the probe as well (17).

Relaxing assumptions

Robustness against experimental noise, which weakens the fundamental assumptions of ptychography is also as important (if not more) as the inversion algorithms. The following algorithms (Class 2) are those that relax these assumptions, which allow ptychography to be experimentally viable.

The simplest of these is to account for random noise. Perhaps hinted by CGD, ptychography can be reformulated as an optimization scheme. It should come as no surprise that a statistical noise model can be incorporated by using Maximum Likelihood Estimation (MLE), shown by Thibault and Guizar-Sicairos (18). MLE can be computationally expensive, however, so PIE or DM can first efficiently sweep the solution space to find probable regions, while MLE can refine the solution.

One improvement that radically improved the quality of reconstruction was the introduction of mixed state ptychography by Thibault and Menzel (19), which relaxes the fundamental assumption of coherence. Introducing mixed states of the probe and object via density matrices, they were able to connect ptychography to quantum tomography. Allowing the beam to be partially coherent can permit much more various and brighter sources of light/electrons to be used.

The multiplicative assumption in real space, and the assumption of known scan positions have also been relaxed by various methods. The former can be tackled by effectively propagating the beam through the sample with multi-slice ptychography (5), effectively achieving volumetric imaging. Probe position refinement (20,21) can be done through various optimization schemes.

References